
„DIE NÄCHSTE BITTE!“
Die achtjährige Luisa, meine nächste Klientin an diesem Tag, besteht darauf, dass ich sie auf diese Art aufrufe, „wie beim Arzt“. Ohne den Spruch bewegt sie sich normalerweise nicht aus dem Wartezimmer heraus. Heute jedoch stürmte sie unter meinem Arm, der die Tür offen hielt, hindurch in den Schulungsraum, noch bevor ich das Ritual Aufruf beendet hatte. Sie setzte sich auf ihrem Platz und rutschte unruhig hin und her.
Luisa ist noch nicht lange bei mir. Sie hatte sich von der reinen symbolischen Betrachtung der Mathematik und damit von der zählenden Ergebnisermittlung nicht lösen können. Mathe war für sie zu einem Buch mit sieben Siegeln geworden, einem magischen Wissen, das nur wenigen vorbehalten zu sein schien. Die zweite Klasse, die Luisa besucht, ist schon weit bis in den Hunderter-Zahlenraum fortgeschritten.
Mit Luisa muss ich, aufgrund der enormen Defizite, die Mathematik neu aufbauen und habe erst kürzlich mit dem Symptomtraining begonnen. Wir befinden uns also noch im Zahlenbereich bis 10, wo es Luisa inzwischen bereits gelingt einfache Terme in Geschichten zu übersetzen und diese mit Material nachzustellen.
Wegen eines Feiertags hatten wir uns zwei Wochen nicht gesehen und offensichtlich gab es etwas zu berichten. Luisa wartete auf ihrem Stuhl ungeduldig auf meine übliche Frage: „Was gibt es Neues?“ Jetzt hielt sie nichts mehr auf dem Stuhl und sie eilte, ohne eine Antwort zu geben, zur Tafel. Das nächstbeste Kreidestück war gerade gut genug und sie zeichnete eine 7-mal-7-Matrix aus Kästchen auf das Board, die sie in großer Eile mit aufsteigenden Zahlen füllte.
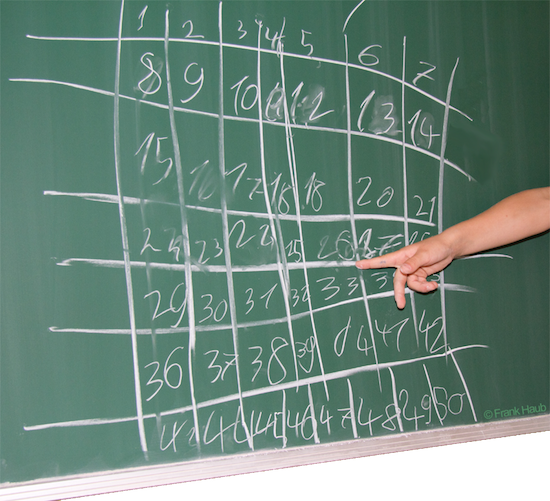
„In der Schule habe ich jetzt gelernt, wie man schnell bis Hundert rechnet“, kommentierte sie ihr Gemälde. „Normalerweise muss ich das nicht immer malen“, sagte sie, „Meine Lehrerin gibt mir ein Blatt, wo das schon drauf ist. Aber du hast so was ja nicht.“
Ich runzelte stumm die Stirn, was sie dazu veranlasste mich zu beruhigen: „Macht nix. Ich zeige dir das jetzt. – Pass auf!“ – Ich passte auf und mich befiel eine beunruhigende Vorahnung. Nachdem die letzte Reihe mit Zahlen gefüllt war, begann Luisa mit ihren Erläuterungen: „Ich muss jetzt zum Beispiel 17 plus 12 rechnen.“ Luisa versuchte sich zu orientieren und fand schließlich das Kästchen mit der siebzehn. „Wegen dem Plus muss ich dann nach unten gehen“, erklärte sie mir, „und zwar einen Schritt, – wegen der 1 in der Zwölf. Verstehst du?“ Mein Schweigen hielt sie nicht davon ab, weiterzumachen. Luisa tippte mit dem Finger auf die Zahl unter der 17. „So! Und jetzt muss ich in die Richtung gehen”, sie deutete nach rechts, „und zwar zwei Schritte, wegen der 2“. Luisa tippte zwei Kästchen nach rechts. „Fertig!“ – Sie erwartete irgendeine Reaktion. „Was liest du denn da, wo ich jetzt hinzeige?“ versuchte sie mir zu helfen und ich las vor: „26?“ – „Ja, genau“, sprudelte sie hervor, „Das ist das Ergebnis. – Sechsundzwanzig!“
Ich war sprachlos. Nicht weil ich ihre Rechenkunst bewunderte, denn das Ergebnis entsprach bei weitem nicht dem, was ich in meinem jahrelangen Mathematikstudium gelernt hatte, sondern weil ich mich einer Situation ausgesetzt sah, bei der einerseits dringender Handlungsbedarf bestand, andererseits aber zu vermeiden war, das stolze Mädchen vor den Kopf zu stoßen.
„Aha! – Wer hat dir denn das gezeigt?“, fragte ich. – „Frau Betterno, meine Mathelehrerin.“ Mit Luisa hatte ich noch nie über die 10 hinaus gerechnet. Die wahrhaftige Bedeutung von Zehner und Einer war ihr genauso wenig geläufig, wie die Strategie der Zehnerüberschreitung. Ich konnte mit ihr also nur auf zählender Ebene diskutieren, mit der Hoffnung, dass sie ihr Missverständnis selbst aufdecken wird. Das Plus-Zeichen hatten wir ja schon erarbeitet. Luisa wusste, dass damit das Zusammenfügen zweier Teile zu einem Ganzen symbolisiert wird. Die beiden dafür infrage kommenden Mengen in ihrem Beispiel entlarvte sie sehr schnell. – Die 17 und die 12. – Ich holte die Box mit den Steckwürfeln und beauftragte Luisa 17 plus 12 mit den Würfeln nachzustellen. „17 Pferde sind auf der Weide und 12 kommen hinzu“, kommentierte sie, als sie die beiden Mengen zusammenschob. Die neue Gesamtmenge zählte sie dann ab. Ich hütete mich, sie abzulenken. Da sie noch nicht bündelte, sagte sie die Zahlenreihe in Einzelschritten auf, wobei sie jeweils einen Würfel aus der zuvor gebildeten Gesamtmenge heraus löste. Jegliche Ablenkung hätte sie aus dem Konzept gebracht, mit der Folge, dass sie von vorne beginnen müsste.
„Neunundzwanzig“, sagte sie schließlich, „hier kommt jetzt auf einmal Neunundzwanzig raus. Eben waren es 26. – Komisch! – Ich zähle besser nochmal!“ Davon konnte ich sie noch abhalten, indem ich ihr versicherte, dass ich genauso viele gezählt hatte und dass wir lieber ihr Tafelgemälde nochmal betrachten sollten. Ihrer Meinung nach stimmte dort aber auch alles. „Aber sonst klappt es doch immer“, zweifelte sie.
Plötzlich fiel ihr ihre kleine Geldbörse ein, der sie einen klein zusammengefalteten Zettel entnahm. „Da! – Das hat Frau Betterno mir gegeben, damit ich überall rechnen kann.“ Sie entfaltete das Papierstück.
Ich erschrak. Da war sie – die befürchtete Hunderter-Tafel. Luisa tippte mit ihrem Zeigefinger auf die 17, tippte dann auf die Zahl eine Reihe darunter und bewegte danach den Finger zwei Schritte nach rechts, als würde sie eine Spielfigur bewegen. So ermittelte sie: „Neunundzwanzig. – Hier kommt jetzt auch neunundzwanzig raus. – Seltsam!“. Mit dem Zettel der Lehrerin schien es zu funktionieren.

Mit dem Zeigefinger auf Zahlen herum tippen und dann eine Zahl als Ergebnis ablesen…. Woran erinnerte mich das? – Genau! Dasselbe macht man bei der Benutzung eines Taschenrechners.
Ohne, dass man verstanden haben muss, was man da eigentlich tut, lässt man ein Schema, einen Bewegungs-Algorithmus, ablaufen und erwartet, dass das abgelesene Resultat richtig ist. Der Papier-Taschenrechner beinhaltete eine Logik, die man erstmal verstanden haben muss. Kleinste Änderungen bei der Nachbildung des “Gerätes” lassen den Ablauf scheitern, wie Luisa eindrucksvoll demonstriert hatte. Bei einem solchen, schematischen Vorgehen ist eine Fehleranalyse, also die Plausibilitätsprüfung des eigenen Ergebnisses unmöglich.
Luisa hat damit gezeigt, dass es nicht reicht, einfach eine Rechenvorschrift einzupauken, ohne dass die Hintergründe verstanden sind. Erst muss man begriffen haben, warum, in Luisas Fall, die Hundertertafel der Lehrerin „funktioniert“, da sie, wie unser Zahlensystem dekadisch strukturiert ist und dass eine lotrechte Bewegung dem Hinzuzählen oder Rückwärtszählen von ganzen Zehnern und dass eine waagerechte Bewegung dem Hinzuzählen oder Rückwärtszählen von Einern entspricht und dass man, wenn die Reihe zu Ende ist, in der nachfolgenden bzw. der vorhergehenden Reihe am anderen Ende weitermacht, weil die Hundertertafel eigentlich ein unterteilter Zahlenstrahl ist. Gerechnet hat man dann trotz allem nicht, sondern lediglich gezählt. Die Zahlen in der Schulmathematik sind aber nun mal keine Positionen auf einem Strahl oder in einer Matrix und die Rechenzeichen Plus und Minus sind keine Bewegungs- oder Zählvorschriften.
Nur wenn man Mathematik als das bloße Ermitteln von Ergebnissen versteht, kann man nachvollziehen, dass jemand den Kindern mit einer ordinalen Zahlenvorstellung einen solchen Papierrechner in die Hand gibt. Denn genau zu einem solchen Taschenrechner wird die Hundertertafel degradiert, wenn sie unverstanden anwendet wird. Die Schul-Mathematik sollte nicht reine Symbolik und Schemata behandeln, sondern Mengen und Mengenhandlungen, die durch die Zahlen und Rechenzeichen repräsentiert werden. Will man die Mathematik verständig vermitteln, muss man den Zusammenhang von Zahlen zu Mengen und von Rechenoperationen zu Handlungen knüpfen. Die Hundertertafel mit ihrer positionellen Zahlendarstellung scheint mir für diese Aufgabe ein wenig kompliziert, wenn nicht gar ungeeignet. Ich bleibe lieber bei meinen Steckwürfeln, die man übrigens, – und das wäre mein Kompromiss-Vorschlag – auch in Form einer Matrix anordnen kann.

Luisas Stunde versuchte ich noch ins Positive zu wenden, indem ich sie die Unterschiede zwischen ihrem Tafel-Kunstwerk und Frau Betternos Hundertertafel herausfinden lies. Luisa hatte Spaß an dem „Suchspiel“, was dann auch eine gute Gelegenheit vorlegte, Luisa erste Einblicke in die dekadische Bündelung zu ermöglichen und ich hörte nach der Verabschiedung, wie sie vor der Praxistür ihrer Freundin, die sie abholte, erklärte, warum man in einer Reihe der Hundertertafel immer 10 Zahlen haben muss.